https://arxiv.org/abs/2204.11115
Time Series Forecasting (TSF) Using Various Deep Learning Models
Time Series Forecasting (TSF) is used to predict the target variables at a future time point based on the learning from previous time points. To keep the problem tractable, learning methods use data from a fixed length window in the past as an explicit inp
arxiv.org
[INDEX]
1. Introduction
2. Methodology
3. Deep Learning Frameworks
4. Data And Experiments
5. Results
6. Conclustions
1. INTRODUCTION
시계열과 시계열 예측
시계열은 일정 기간 동안 주어진 m개 변수의 반복된 관측값의 시퀀스다. 시계열 예측은 과거 관측치를 기반으로 미래 시점에서 타겟 변수의 분포를 예측하는 데에 사용된다.
시계열을 분석하는 모델의 3가지 카테고리
1. Traditional models
[선형 모델]
정상성을 가진 시계열을 해결할 수 있는 Autoregressive Moving Averate(ARMA)와 비정상성을 가진 시계열을 해결할 수 있는 Autoregressive Integrated Moving Average(ARIMA)이 대표적이다. ARIMA의 변형에는 Autoregressive Fractionally Integrated Moving Average (ARFIMA)와 Seasonal Autoregressive Integrated Moving Average (SARIMA)가 포함된다.
[비선형 모델]
비선형 모델 중에서는 Autoregressive Conditional Heteroskedasticity (ARCH)와 그 변형인 Generalized ARCH (GARCH), Exponential Generalized ARCH (EGARCH), Threshold Autoregressive (TAR), Non-linear Autoregressive (NAR), Non-linear Moving Average (NMA) 등이 있다.
전통적 모델의 한계점은 3가지로 요약할 수 있다.
(1) 가장 최근의 데이터로부터 고정된 요인 집합에 회귀를 적용하여 예측을 함
(2) 전통적 방법은 반복적이며 프로세스가 어떻게 시작되는지에 민감할 수 있음
(3) 정상성은 엄격한 조건이기 때문에 단순히 드리프트(drift), 계절성(seasonality), 자기상관성(autocorrelation) 및 이분산성(heteroskedasticity)를 해결하는 것만으로 변동성이 큰 시계열의 정상성을 달성하기는 어려움
2. Standard machine learning models
Support Vector Machines (SVM)과 같은 표준 기계 학습 모델이 사용되었으며, ARIMA와 SVM 또는 Neural Networks와 결합된 하이브리드 접근 방식도 사용되었다.
3. Deep learning models
인공 신경망 (ANN)과 딥러닝 신경망은 전통적인 방법보다 성능이 더 좋다는 것이 입증되었다.Recurrent Neural Network (RNN), Long Short-term Memory (LSTM), 그리고 GRUs은 시곙려 예측에 적합한 모델에 속하며, Attention 기반의 메서드인 Transformers를 사용하여 예측이 개선되기도 했다.
논문의 목표
(1) 시계열 예측을 위해 딥러닝 모델 (RNN, LSTM, GRU, Transformer)을 적용하고 검증하며 각각의 성능을 비교
(2) 모델의 장단점을 평가
(3) look-back 창의 크기와 미래 예측의 기간이 예측 정확도에 미치는 영향을 이해
사용된 데이터셋
UCI website의 Beijing Air Quality 데이터셋 (2010 ~ 2014)
2. METHODOLOGY
과거 데이터를 사용하여 딥러닝 모델이 미래 시점의 대상 변수를 예측하는 방법
과거 데이터를 사용하여, 딥러닝 모델은 입력 특성과 대상 변수의 미래 값 사이의 기능적 관계를 학습한다. 이 결과 모델은 미래 시점에서 대상 변수에 대한 예측을 할 수 있다. 모델의 입력을 균일한 길이로 만들기 위해, 크기가 W인 고정 길이의 sliding time window를 사용할 수 있다.

look-back size와 look-ahead size

look-back size w를 통해 얼만큼의 과거 데이터를 가져올 것인지 정할 수 있으며(input data), input data로부터 얼만큼의 미래를 예측할 것인지(output data)는 look-ahed size k를 통해 정할 수 있다. 즉, w size만큼의 시계열 데이터를 입력으로 받아 k개 만큼의 미래를 예측하는 것이다. 이러한 w와 k를 통해 훈련 데이터셋을 구축한다.
3. DEEP LEARNING FRAMEWORKS
Recurrent Neural Networks (RNN)

RNN은 시계열 데이터를 모델링하는 데 가장 적합하다. RNN은 입력 특성과 미래의 대상 변수 간의 기능적 관계를 모델링하기 위해 신경망을 사용한다.
RNN은 t-1 시점부터 t시점까지의 internal (hidden) state의 전이에 집중하여 과거 데이터의 훈련 세트에서 재귀적으로 학습한다. 그 결과 모델은 세 개의 매개변수 행렬 Wx, Wy, Ws과 두 개의 바이어스 벡터 bs, by로 결정되며, 이들은 모델을 정의하는 데 도움을 준다. 최종 출력물인 yt는 internal state인 St에 의존하며, 이는 현재 인풋 Xt와 이전 state st-1에 의존하는 것이다.


St는 과거의 여러 시간 단계에서부터 지속적으로 수집된 데이터를 사용하여 생성되는 벡터이며, 컨베이어 벨트 역할을 하는 mainstream이다.
즉, RNN은 과거 시점들의 데이터를 지속적으로 갱신하면서 현재 시점의 데이터와 함께 고려하여 예측하고, main stream을 지속적으로 갱신해 나가는 방식으로 작동한다. 과거 정보와 현재 데이터를 반영한 셀 상태는 다음 시점의 데이터를 예측하기 위해 다시 입력되며, 이러한 재귀적인 방식은 정보를 지속적으로 업데이트하는 메커니즘으로 작용한다.
RNN의 문제점
RNN의 가장 큰 단점은 재귀적 가중치 행렬의 반복 곱셈으로 인해 gradient vanishing problem이 발생한다는 것이다. 이는 gradient가 시간이 지남에 따라 너무 작아져서 RNN이 정보를 작은 기간 동안만 기억하게 되기 때문에 발생한다.
Long Short-term Model (LSTM)
LSTM은 RNN의 변형으로, gradient vanishing 문제를 부분적으로 해결하고 시계열 데이터의 장기 의존성을 학습한다.

LSTM은 t 시점을 internal (hidden) state St와 cell state Ct로 표현한다. Ct에는 3가지 다른 종속성이 있다. 이는 이전 cell state Ct-1, 이전의 internal state St-1, 현재 시간 xt의 input이다.
Fig 4에 나타나있는 프로세스는 망각 게이트, 입력 게이트, 출력 게이트 및 추가 게이트를 사용하여 정보를 제거/필터링, 곱셈/결합 및 추가하는 것을 허용한다. 이를 통해 장기 의존성을 더 세밀하게 제어할 수 있다.
Gated Recurrent Unit(GRU)
GRU는 LSTM의 변형으로, gradient vanishing 문제를 보다 적극적으로 해결하기 위한 것이다. 복잡한 LSTM 모델을 좀 더 단순화하여 파라미터 개수를 줄인 것이라고 볼 수 있다.

GRU의 새로운 점은 update gate(function zt), reset gate(function rt), third gate(function St)를 사용한다는 점이다. 각각의 게이트는 이전 정보를 어떻게 필터링하고, 사용하고, 결합할지 제어하는 역할을 한다.
zt는 현재 정보의 중요도를 나타내며, (1-zt)는 과거 정보의 중요도를 나타낸다. 이 (1-zt)에 St-1을 곱한 값은 과거로부터 무엇을 잊지 않을지 결정한다. 반면 zt에 St를 곱한 값은 현재 정보에서 무엇을 보유할지 결정한다.
Transformer Model
LSTM과 GRU는 기울기 소실 문제를 어느 정도 해결하지만, 여전히 하이퍼볼릭 탄젠트와 시그모이드 함수를 활성화 함수로 사용하기 때문에 깊은 층에서 기울기 소실 문제가 여전히 발생합니다.
이에 반해 transformer는 과거에서 중요한 정보를 선택적으로 가중치를 부여할 수 있는 attention을 활용하여 시계열에서 최고의 성능을 보인다. attention 기능은 중요한 특징과 과거의 경향에 주의를 기울이도록 도와준다.

transformer는 encoder와 decoder로 구성되어 있다. k는 예측할 날의 수 (output data)를 의미하고, w는 얼만큼의 과거 데이터를 가져올 것인지 (input data)를 뜻한다. decoder에는 Masked Attention mechanism과 encoder output 중에서 선택된 피처 벡터를 사용하는 Multi-Head Attention mechanism이 포함되어 있다.
또한, transformer는 positional encoding을 사용하여 데이터의 시간 순서를 포함한다. encoder는 w 크기 만큼의 데이터를 받아 디코더에서 사용될 feature vector를 출력한다. 훈련 과정에서 decoder는 k만큼의 미래 데이터도 입력받는다.
4. DATA AND EXPERIMENTS
Dataset
UCI 웹사이트의 Beijing Air Quality Dataset을 활용하여 실험이 진행되었다. 이 데이터셋은 2010년부터 2014년까지의 데이터를 포함되어 있다. Min-Max normalization을 실행했고, 범주형 데이터 컬럼에 대해서는 One-hot embedding이 사용되었다.

처음 70% 행은 training set, 나머지 30%의 행은 test set에 해당된다.
Experiements
두 가지의 실험이 진행되었다.
1. Single step: 다음 시점을 이전 시점의 데이터를 사용하여 예측 (k = 1)
2. Multi step: 다음 여러 시점을 이전 시점의 데이터를 사용하여 예측 (k > 1)
두 실험에서 모두 window size로는 1, 2, 4, 8, 16일이 사용되었다.
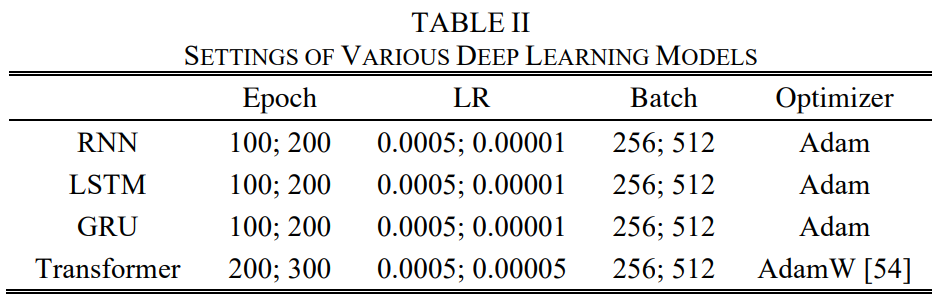
실험에서 사용된 4개의 모델에 설정된 파라미터는 위과 같다.
Measures of Evaluation
손실함수로는 평균 제곱 오차(MSE, Mean Squared Error)를 사용하였다.
5. RESULTS
Predict Multiple Timesteps Ahead
고정된 look-back window 크기 w에 대해, look-ahead 크기 k를 증가시킬수록 모델 성능이 어떻게 악화되는지 실험해보았다. 아래의 결과 표에서 볼 수 있듯이 k가 증가함에 따라 MAE와 RMSE 값이 증가했다. 실험을 통해 트랜스포머 모델은 실험의 80%에서 RNN, LSTM 및 GRU보다 성능이 우수한 것을 확인할 수 있었다. 또한, 미래 4시간 이상을 예측해야 할 때 예측 성능이 급격히 저하되었다.


Different Look-back Window Sizes
Multi-step predictions
transformer 모델은 더 큰 k값에 대해 다른 모델보다 우수한 성능을 보여주는데, 이는 attention을 사용했기 때문이라고 볼 수 있다. look-back window 크기 w가 작을 때에는 GRU와 LSTM이 RNN보다 더 우수한 성능을 보이는데, 이는 GRU와 LSTM이 RNN보다 더 긴 기간의 기억을 가지고 있으며, 기울기 소실 문제를 일부 해결했기 때문이라고 예측할 수 있다. 즉, single-step에서 window 사이즈가 작을 때에는 LSTM과 GRU가 좋은 성능을 보였다. 반면 transformer는 window size가 클 때도 더 나은 성능을 보이진 못했다. 이는 큰 window 크기로 인해 노이즈 수준이 증가하여 발생한 것일 수 있다.
Multi-step predictions
이 실험에서는 transformer가 다른 모델들보다 우수한 성능을 보인다.


5. CONCLUSIONS
- transformer 모델은 먼 미래를 예측할 때 가장 우수한 성능을 보이며, LSTM와 GRU는 단기간 예측에 RNN보다 우수한 성능을 보인다.
- single-step prediction에서 window 크기의 최적값은 w = 24시간이다. multi-step prediction의 경우, 최적값은 w = 48 또는 96시간이다. (k = 3시간일 때)
- multi-step prediction의 경우, transformer가 다른 방법보다 우수한 성능을 보였지만, single-step prediction의 경우 transformer는 look-back 창이 클 때만 잘 작동했다. GRU와 LSTM은 더 작은 w 값에 대해 더 우수한 성능을 보였다.
