Logistic Regression
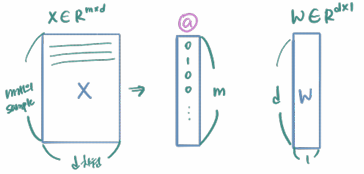
- 차원의 mm개 샘플을 입력받아 d×1 크기의 가중치 W와 내적한 뒤, 시그모이드 함수를 통해 0과 1 사이의 값이 출력됨
- 주로 이진 분류를 하는 데에 사용됨

- Hypothesis는 시그모이드 함수 형태를 따르며, 항상 0과 1 사이의 값이 출력됨
- 출력값에 임계값을 지정하여 이를 0 혹은 1로 분류하는 데 사용됨
- H(X)는 어떤 입력 X가 정답(1)일 확률을 나타냄
Cost Function

- W는 학습 가능한 파라미터(가중치)이며, 이에 따라 cost함수의 값이 결정됨
- cost 함수는 전체 데이터에 대해 평균을 내며, 모델이 얼마나 잘 예측했는지를 평가함
- cost 함수는 모델이 예측한 확률 $H(X)$와 실제 정답 y 사이의 차이를 예측함
- 가 H(X)와 가까울수록, cost 값은 0에 가까워짐
- 와 H(X) 값이 다를수록, cost 값은 커짐
- 주로 경사하강법을 통해 cost를 최소화하는 방향으로 W를 업데이트함
- log 함수는 예측이 정답과 다를수록 페널티를 더 크게 주기 때문에 사용

- cost 함수는 위의 코드와 같이 효현할 수 있음
- 정답인 y가 1일 떄에는 첫째 항만 남게 됨 → cost 함수의 값은 $-log(h(x_i))$가 됨 → $h(x_i)$ 값이 1에 가까워야 cost가 작아짐
- 정답인 y가 0일 때에는 둘째 항만 남게 됨 → cost 함수의 값은 $-log(1 - h(x_i))$가 됨 → $h(x_i)$ 값이 0에 가까울 수록 cost가 작아짐
- 정답에 가까운 예측일수록 cost가 작아지고, 이는 학습이 잘 되었다는 뜻임

- α는 학습률을 의미하며, 이는 한 번의 업데이트로 얼마나 크게 이동할지를 결정함
- cost 함수가 줄어드는 방향으로 W를 조금씩 이동시키며 학습을 진행함
- 예시
- cost 함수로 W를 미분했을 때 3의 값이 나왔음
- 이는 W를 아주 조금 증가시키면, cost 함수의 값이 약 3만큼 증가한다는 뜻
- 즉, 이 방향은 cost가 점점 커지는 방향이라는 뜻
- cost를 줄여야하기 때문에 해당 기울기(3)가 가리키는 방향 의 반대 방향으로 가야 함

[그림 출처]
모두를 위한 딥러닝 시즌2 slide: https://drive.google.com/drive/folders/1qVcF8-tx9LexdDT-IY6qOnHc8ekDoL03