https://arxiv.org/abs/1706.03762
Attention Is All You Need
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new
arxiv.org
1. Introduction
RNN(순환 신경망)이나 LSTM(장단기 메모리), Gated Recurrent Nerual Network(게이트 순환 신경망)은 시퀀스 모델링과 transductive learning에서 SOTA 모델로 자리잡았다.

하지만 이러한 RNN의 가장 큰 문제점은 입력 문장을 하나의 고정된 context vector에 압축해야 한다는 점이다. 또한, RNN의 순차적인 계산 방식은 학습 과정에서 병렬 처리를 어렵게 만들어 효율성을 저하시킨다.
이러한 한계를 해결하기 위해 Attention 메커니즘이 등장했다. Attention은 입력 문장의 각 단어에 대한 정보를 매번 동적으로 활용하며, 순환성을 완전히 배제한 구조를 통해 병렬 처리를 가능하게 한 것이 가장 큰 특징이다.
2. Background
CNN 기반의 병렬 처리 모델로 순차적 계산을 줄이려는 노력이 있었지만, 위치 간 거리가 멀어질수록 의존성을 학습하기 어려운 한계가 있다. Transformer는 셀프 어텐션을 사용하여 입력 시퀀스 길이에 관계없이 모든 위치 간의 관계를 한꺼번에 계산하여 상수 시간으로 계산을 끝낼 수 있었다. 하지만 각 단어의 표현을 계산할 때 입력 시퀀스의 모든 단어의 정보를 가중합으로 통합한다는 문제가 있었고, 이는 멀티 헤드 어텐션을 통해 해결할 수 있었다. Transformer는 이를 단독으로 활용하여 RNN이나 CNN 없이도 입력과 출력의 표현을 계산하는 최초의 모델이 되었다.
3. Model Architecture
Transformer의 전체적인 아키텍처는 아래와 같다.
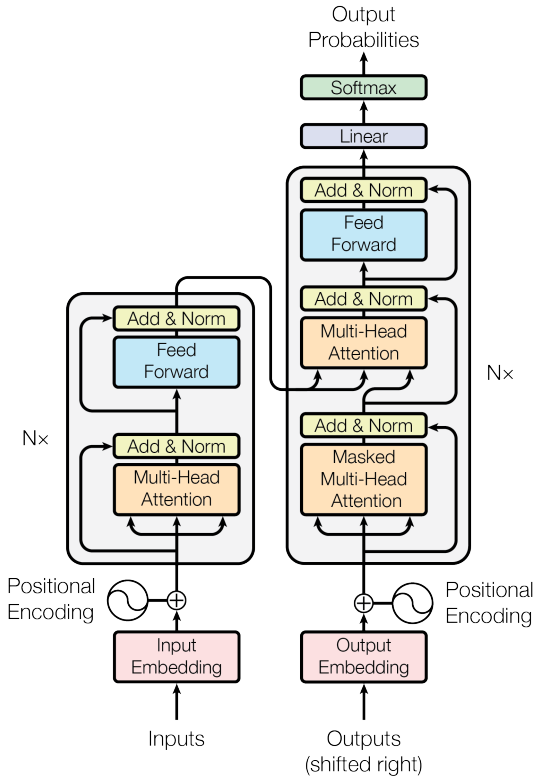
3.1 Encoder and Decoder Stacks
Encoder
디코더의 세부적인 구조를 살펴보기 전에, transformer의 핵심 메커니즘인 Attention에 대해 알아보고자 한다.
Attention의 기본 원리


- 임베딩 벡터로 표현된 각 단어와 디코더의 현재 은닉상태 $dh_1$의 각각을 내적하여 유사도 점수(Alignment Scores)를 계산한다. 이후, 이 유사도 점수에 softmax 함수를 적용하여 Attention Weights를 구한다. Attention Weight는 항상 합이 1로, 해당 토큰을 예측하는 데에, 입력 토큰 각각의 중요도를 표현해준다.
- 토큰 각각에 대한 임베딩 벡터를 Attention Weights와 각각 곱한 후, 이 값들을 더해 가중합(Weighted Sum)을 구한다. 이는 context vector가 된다.
- context vector $C_t$와 디코더 상태 $S_t$를 결합하여 새로운 상태인 $\tilde{s_t}$를 계산한다. 갱신된 상태 $\tilde{s_t}$를 사용해 Softmax로 다음 단어의 확률 분포를 생성한다. 최종적으로 $ \hat{y_t} $에서 가장 높은 확률을 가진 단어를 선택해 다음 단어로 출력한다.
Encoder의 input
Input Embedding
문장의 각 시퀀스(토큰)를 학습에 사용되는 벡터로 임베딩하는 임베딩 layer은 아래와 같다.
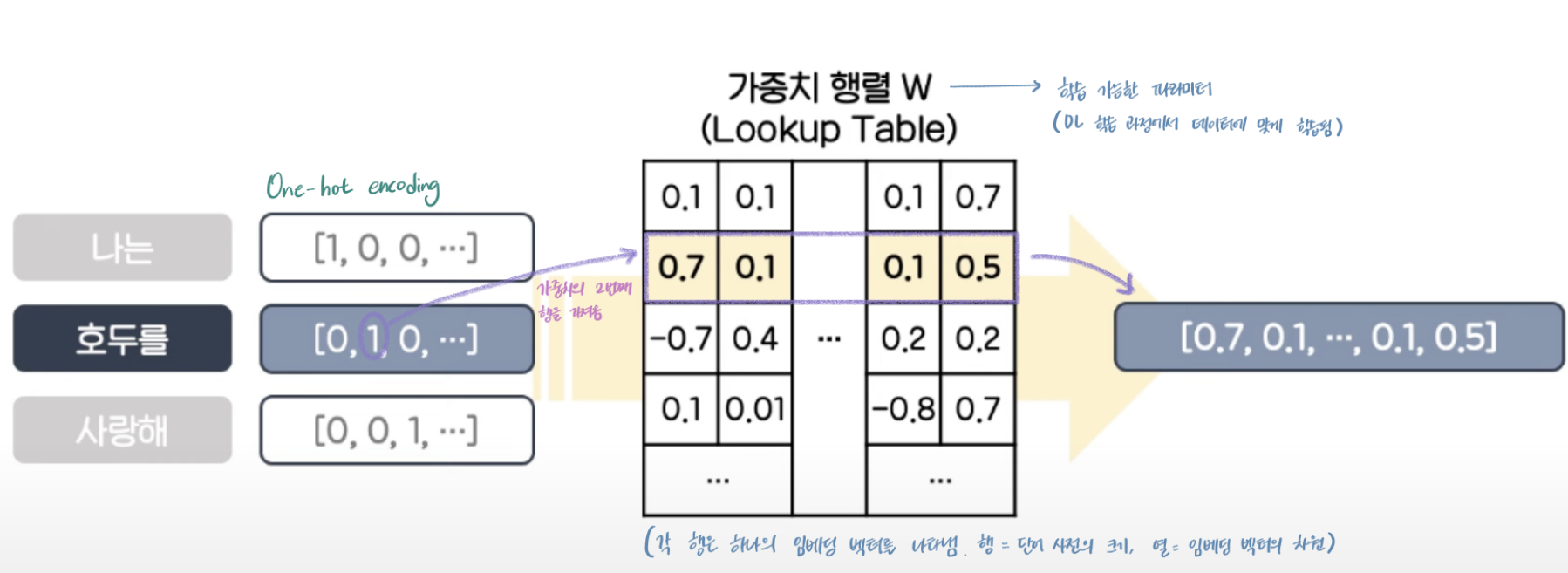
각 토큰은 One-Hot Encoding으로 표현된 벡터에서 1의 위치를 인덱스로 사용하여 가중치 행렬 W의 해당 행을 가져온다.
가중치 행렬W에서 각 행은 하나의 임베딩 벡터를 나타내기 때문에 행은 단어 사전의 크기를 나타내고, 열은 고정된 모델의 임베딩 벡터의 차원을 나타낸다.
Positional Encoding
순차적으로 토큰이 처리되는 순환 신경망과 달리, Transformer는 입력 시퀀스의 모든 토큰을 병렬로 처리하기 때문에 위치 정보가 모델에 직접적으로 포함되지 않는다. 이를 해결하기 위해 Positional Encoding을 사용한다.

Transformer에서는 입력 시퀀스를 한 번에 모두 처리하기 때문에, 기존 Seq2Seq 구조와 달리 토큰의 순서 정보가 자연스럽게 보존되지 않는다. 따라서 각 토큰의 위치를 명시적으로 표현해주기 위해 입력 임베딩에 위치 정보를 인코딩한 벡터(Positional Encoding)를 더한다. 이 인코딩은 각 위치마다 유일한 값을 가지며, 토큰 간 위치 차이가 일정한 의미를 가지도록 설계되어 있다.


단순히 pos = 1, 2, 3... 식으로 넣으면 모델이 일반화하기 어렵고, 위치 간 차이를 정량적으로 인식하지 못한다. 대신 다양한 주기의 sin/cos 함수를 사용하면 서로 다른 위치는 고유한 벡터로 표현되고 가까운 위치는 비슷한 벡터를 가지게 되어 모델이 위치 정보를 자연스럽게 학습할 수 있다.
Positional Encoding은 입력 토큰의 순서 정보를 벡터로 표현하여, 모델이 시퀀스 내 위치 관계를 학습할 수 있도록 돕는다.
각 입력 토큰은 임베딩 벡터로 변환된 뒤, Positional Encoding 벡터와 합산된다. 이때 완성된 벡터들은 결합되어 입력 시퀀스 전체를 나타내는 하나의 행렬로 변환되어 인코더에 입력된다.

https://www.blossominkyung.com/deeplearning/transfomer-positional-encoding
트랜스포머(Transformer) 파헤치기—1. Positional Encoding
트랜스포머 Transformer Attention is All You Need Postional Encoding
www.blossominkyung.com
참고
Scaled Dot-Product Attention
Matrix Multiplication
이제는 Scaled Dot-Product Attention의 과정을 하나씩 살펴보고자 한다. 프로세스는 아래와 같다.

가장 먼저 이뤄지는 것은 Query와 Key 간의 Matrix Multiplication이다.

- 위의 그림에서 Query(검색어)와 가장 유사한 Key는 Key2이다.
- 전체 Key 중 Query에 대해 각 Key들이 지니는 비중(유사도)를 계산 = [$a_1$, $a_2$, $a_3$, $a_4$]
- 각각의 유사도와 Value를 곱한 값의 합을 구함 = $a_1$[0.1, 0.5] + $a_2$[-0.1, 0.7] + $a_3$[-0.9, 0.1] + $a_4$[0.0, -0.8]
- 위 계산의 결과는 결국 Query와 가장 관련이 깊은 Key의 Value 위주로 모든 값을 가져오는 것을 의미하고, 이를 Attention이라고 한다. Self Attention인 이유는, 자기 자신을 포함한 모든 Key의 Value를 가져오기 때문이다.
앞서 완성된 입력 임베딩 행렬은 아래와 같이 copy하여 총 3개의 행렬로 만든다.

copy된 3개의 행렬은 각각 Query, Key, Value 가중치 매트릭스가 된다. 이때, 가중치 매트릭스는 Transformer에서 학습이 가능한 trainable parameter로서 생성되는 것이다.
각각의 매트릭스는 아래의 사진과 같이 입력 임베딩 매트릭스와 내적을 하여 Query, Key, Value 행렬을 생성한다.

Dot product attention은 아래와 같이 계산된다.
먼저 Query와 transpose된 Key 행렬의 곱을 구한다. 이 과정에서 $Q$의 행 벡터를 $ K^T$의 열 벡터와 곱하여 각 Query에 대한 Key의 유사도를 계산한다. 이 유사도는 각 Query가 Key에 얼마나 집중할지를 나타내며, 이후 Softmax를 통해 확률 분포로 변환된다.
($Q$의 각 행 벡터를 $ K^T$의 각 열 벡터와 내적한 후, 이 내적 값들로 구성된 유사도 행렬이 완성된다.)

Scaling
계산된 Matrix Multiplication에 대하여 scaling이 진행된다. 이는 모델의 고정된 임베딩 크기가 클 경우, 내적값이 굉장히 커짐에 따라 특정 softmax 값(가중치)이 1에 가깝워지기 때문이다. 특정 값에 집중되면, 역전파 때 기울기가 매우 작아질 수 있기 때문에 gradient가 소실되는 결과를 낳게 된다.
cf) softmax는 입력값의 차이가 클수록 출력 분포가 특정 값에 강하게 몰리는 특성이 있다.
ex) softmax([10, 0, -10]) ⇒ [0.999, 0.001, 0.00]처럼 한 쪽으로 편향된 결과를 냄

Self Attention 과정 핵심 요약
- Query와 Key를 내적하여, 각 토큰(Query)이 다른 토큰(Key)들과 얼마나 관련 있는지를 나타내는 유사도 점수(Attention Weights)를 계산
- 이를 통해 각 토큰은 자기 자신을 포함한 다른 모든 토큰과의 상대적 중요도 파악 가능
- Attention Weights는 각 Key에 대응되는 Value에 곱해져, 관련 있는 정보일수록 더 많이 반영되도록 가중합된 벡터를 만듦 (Attention Weights의 크기는 [시퀀스 길이 x 시퀀스 길이], Value의 크기는 [시퀀스 길이 x 임베딩 차원]이므로, 행렬 곱을 통해 각 Query 위치에 해당하는 문맥 정보 벡터를 계산한다고 보면 됨)
- 최종적으로 계산된 행렬(Attention Weight와 Value 곱의 결과)은 문장 속 각 단어가 전체 문맥을 고려해 다시 표현된 벡터들의 집합이라고 볼 수 있음
Masking
Padding은 Transformer 모델에서 입력 문장이나 시퀀스의 길이를 맞추기 위해 사용된다.
(단일 문장을 처리하거나 배치 처리 없이 하나의 입력만 사용하는 경우라면 패딩이 없어도 문제 없음)

Softmax
필요할 경우, masking 단계를 거친 Attention Weight는 softmax 함수를 거쳐 확률분포가 된다. Softmax 함수는 각 토큰에 대한 가중치가 0에서 1 사이의 값을 가지게 하고, 이들의 합이 1이 되게 한다. 이렇게 완성된 Attention Weight는 입력 시퀀스의 각 토큰이 얼마나 중요한지에 대한 확률적 가중치를 나타낸다.
Matrix Multiplication
마지막으로 Attention Weights와 Value 행렬을 곱하여 최종 Attention 출력값을 완성한다. 이는 Context vector라고도 불리며, 인코더에 입력되는 행렬과 크기가 동일하다.

Multi-head Attention
멀티헤드 어텐션은 각각의 Query, Key, Value 매트릭스를 지정된 헤드의 개수에 따라 나누어, 병렬로 독립적인 Attention을 수행하는 방식이다.
이를 통해 정보를 병렬로 학습하여 모델이 입력 간의 다양한 관계(ex. 문맥, 어휘적 유사성, 구문적 패턴 등)를 효과적으로 포착할 수 있다.
이 논문에서는 고정된 임베딩 사이즈가 512이고, 헤드의 개수가 8이기 때문에 $d_k$가 64가 된다.
(아래의 예시 사진에서는 고정된 임베딩 사이즈가 4, 헤드의 개수가 2이기 때문에 $d_k$가 2가 됨)

멀티헤드 어텐션이 적용되면, Query, Key 매트릭스는 지정된 헤드 수만큼 나뉘어 각 헤드에서 독립적으로 연산이 수행된다.

해당 과정을 통해 얻은 매트릭스에 softmax를 적용하여 Attention Weight가 만들어진 후에는 Value 매트릭스와 곱해진다.
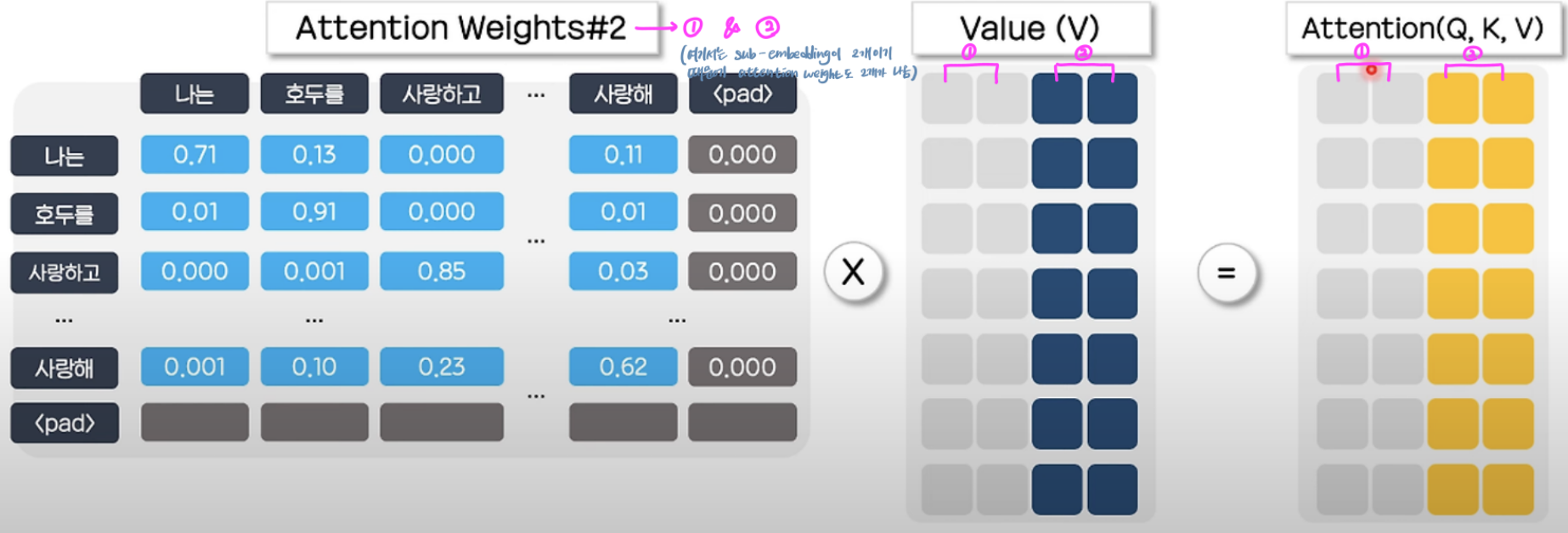
각각의 결과값(매트릭스)는 합쳐져 Attention 매커니즘의 결과물인 contenxt 매트릭스가 되어 다음 레이어의 입력으로 사용된다.

이 사진처럼 멀티헤드 어텐션을 수행하면 단일 헤드 어텐션보다 더 풍부한 관계를 학습할 수 있다. 이는 각 헤드가 다른 입력 단어들 간의 관계를 학습하고, 이 과정을 병렬로 수행하여 문맥 정보와 구조적 정보를 동시에 효과적으로 포착하기 때문이다.
반면, 단일 어텐션은 고정된 임베딩 차원에서 모든 입력이 관계를 학습하기 때문에 다양한 의미적 관계를 동시에 학습하는 데 제한적임
(각 단어가 쿼리 단어에 대해 얼마나 관련 있는지를 알아보기 위해 $QK^T$ 연산을 수행할 때, Q와 K 전체 매트릭스가 한번에 계산되기 때문)

Feed Forward Network

Feed Forward 층은 비선형 변환(ReLU 함수)을 통해 모델의 표현력을 높이는 데 중요한 역할을 한다.
- $W_1$, $W_2$: 학습 가능한 가중치 행렬
- $b_1$, $b_2$: 학습 가능한 편향 벡터
- $max(0, z)$: ReLU 활성화 함수
- $x$: Attention 층으로부터 전달된 입력

Add & Normalization


※ 본 글은 DSBA 연구실의 『[Paper Review] Attention is All You Need (Transformer)』 영상을 참고하여 정리한 내용입니다.
사용된 이미지 또한 해당 영상의 자료를 활용하였습니다.
'Deep Learning > NLP' 카테고리의 다른 글
| [강의 정리] Seq2Seq Learning (0) | 2025.05.08 |
|---|---|
| [논문 리뷰] Efficient Estimation of Word Representations in Vector Space (0) | 2025.03.04 |
| [논문 리뷰] Labeled LDA: A supervised topic model for credit attribution inmulti-labeled corpora (0) | 2024.12.20 |
| [강의 정리] CS224n 1. Introduction and Word Vectors (1) | 2024.11.15 |
| RAG vs. ICL (2) | 2024.10.07 |



